MixMatch与FixMatch论文解读

开场白

做模式识别课内作业，有关MixMatch和FixMatch。

来阅读一下《MixMatch: A Holistic Approach to Semi-Supervised Learning》和《FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence》两篇原论文。

（*＾-＾ *）

原论文阅读

MixMatch

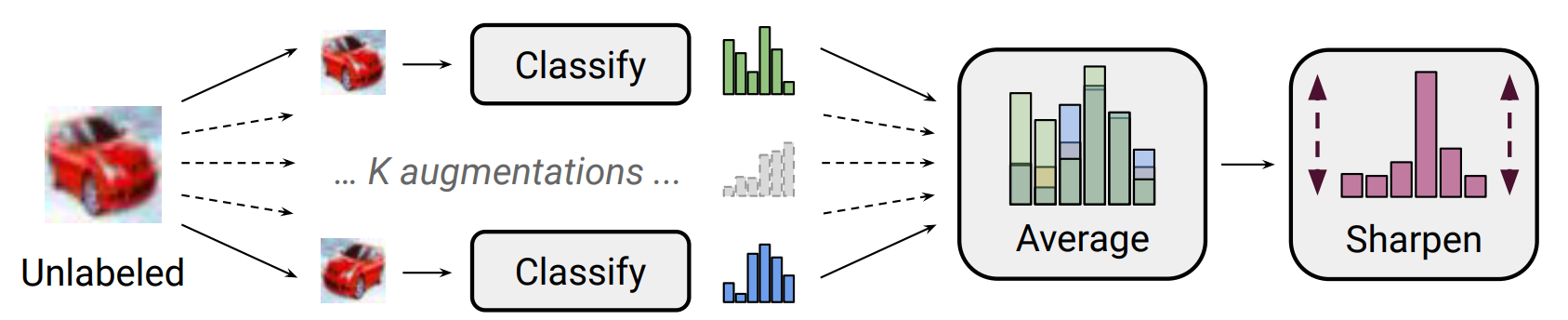
Consistency Regularization

MixMatch使用了一致性正则化(自洽正则化)，即对无标签数据进行数据增广，产生的新数据输入分类器，预测结果应保持一致。

基于这个思想，可以构造出如下损失项：

$$||Pmodel(y | Augment(x); θ) − Pmodel(y | Augment(x); θ)||_2^2$$

$Augment(x)$表示随机的数据增强，因此包含其的两个子项是等价的。

数据增强：对图像做随机平移，缩放，旋转，扭曲，剪切等操作。这里的MixMatch使用了random horizontal flips and crops(随机水平翻转和剪切的数据增强方法)。

Entropy Minimization

MixMatch采用了熵最小化思路，即最小化对无标签数据$x$的$Pmodel(y | x; θ)$​的熵。具体的实现方法是通过Sharpening函数最小化未标记数据的熵。

Traditional Regularization

对模型参数做L2正则化。

同时使用了MixUp方法作为正则化器(应用于标记数据点)兼半监督学习方法(应用于无标号数据点)。

核心方法

针对一个 Batch 的有标签数据 $X$ 和一个 Batch 的无标签数据 $U$ 做数据增广，分别得到一个 Batch 大小的增广数据 $X'$ 和一个$K$倍Batch大小的增广数据 $U'$(这里原论文写的是一个而非$K$个，有歧义)。并利用两批增广后的数据得到两个损失项，通过一个比例组成总的损失项。

具体公式如下：

$$X', U' = MixMatch(X , U, T, K, α)\\ L_X =\frac{1}{|X'|}\Sigma_{x,p∈X'}H(p, Pmodel(y | x; θ)) \\ L_U =\frac{1}{L|U'|}\Sigma_{u,q∈U'}||q − Pmodel(y | u; θ)||^2_2\\ L = L_X + λ_UL_U$$

$H(p, q) $表示$p$与$q$之间的交叉熵。$T、K、\alpha$​为超参数。$L$为类别数。

$MixMatch$函数的具体过程下述。

数据增强、类别猜测以及锐化函数

对于有标签数据$X'$里每个数据的增强只进行一次(对应标签不变)，而对于无标签数据$U'$里的每个数据则会分别进行$K$次，并进行标签猜测。

即将猜测出的类别记为$q_b$，$q_b$的获得过程如下：

$$\overline{q_b} = \frac{1}{K}\Sigma^K_{k=1}Pmodel(y|Augment(u_b),k ; θ) \\ q_b = Sharpen(\overline{q_b}, T)$$

$u_b$表示$U'$里第$b$个数据。关于$Sharpen$函数的定义如下：

$$Sharpen(p, T)_i := \frac{p_i^\frac{1}{T}}{\Sigma^L_{j=1}p_j^\frac{1}{T}}$$

$p$为类别概率，$T$为温度参数。调节$T$趋近于0，得到的$Sharpen(p, T)_i$​就会趋近于"one-hot"分布。而"one-hot"分布的熵会比锐化前要低得多。

这里得到了$K$个Batch的增广数据 $U'$，只不过由同一个原数据$u_b$增广得到的$K$个数据同时共用一个伪标签$q_b$​。

这个共用伪标签的点只看原文不好理解，看了流程图Algorithm 1才明白的。

MixUp步

MixMatch稍微修改了MixUp方法，用以计算两个数据的混合数据：

$$λ ∼ Beta(α, α) \\ λ' = max(λ, 1 − λ) \\ x' = λ'x_1 + (1 − λ')x_2 \\ p' = λ'p_1 + (1 − λ')p_2$$

超参数$\alpha$用于改变$\lambda$的分布，通过 Beta 函数抽样得到权重因子$\lambda'$。

其中第二行公式是MixMatch对MixUp的优化，目的是使得$\lambda'$偏向于1，即让$x'$相较于$x_2$更偏向于$x_1$。

收集前面获得的“(增广数据，标签)”数对如下：

$$\hat{X} = ((\hat{x_b}, p_b); b ∈ (1,...,B)) \\ \hat{U} = ((\hat{u_b}, k, q_b); b ∈ (1,...,B), k ∈ (1,...,K))$$

将$\hat{X}$和$\hat{U}$混合并洗乱得到数据集$W$，长度为$K + 1$个Batch。

然后将$W$中的前Batch个数据与$\hat{X}$中的每个数据进行MixUp得到$X'$，同时将$W$中剩余$K$个数据与$\hat{U}$中的每个数据进行MixUp得到$U'$​。

至此，MixMatch得到了一个 Batch 大小的增广数据 $X'$ 和一个$K$倍Batch大小的增广数据 $U'$​。这一部分的算法如图：

损失函数以及超参数

观察两个损失项：

$$L_X =\frac{1}{|X'|}\Sigma_{x,p∈X'}H(p, Pmodel(y | x; θ)) \\ L_U =\frac{1}{L|U'|}\Sigma_{u,q∈U'}||q − Pmodel(y | u; θ)||^2_2$$

$|X'|$等于Batch大小，$|U'|$等于$K$倍Batch大小。

对于有标签数据采用交叉熵损失，对于无标签数据采取L2损失。这是因为对比交叉熵损失，L2是有界且敏感的，更适合无监督学习。

最终的损失值为两者的加权和：

$$L = L_X + λ_UL_U$$

在原论文中，各个超参数的配置如下：

$\lambda_U$	$T$	$K$	$\alpha$
75 for cifar10	0.5	2	0.75

如上是原论文Experiments部分以前的内容。

FixMatch

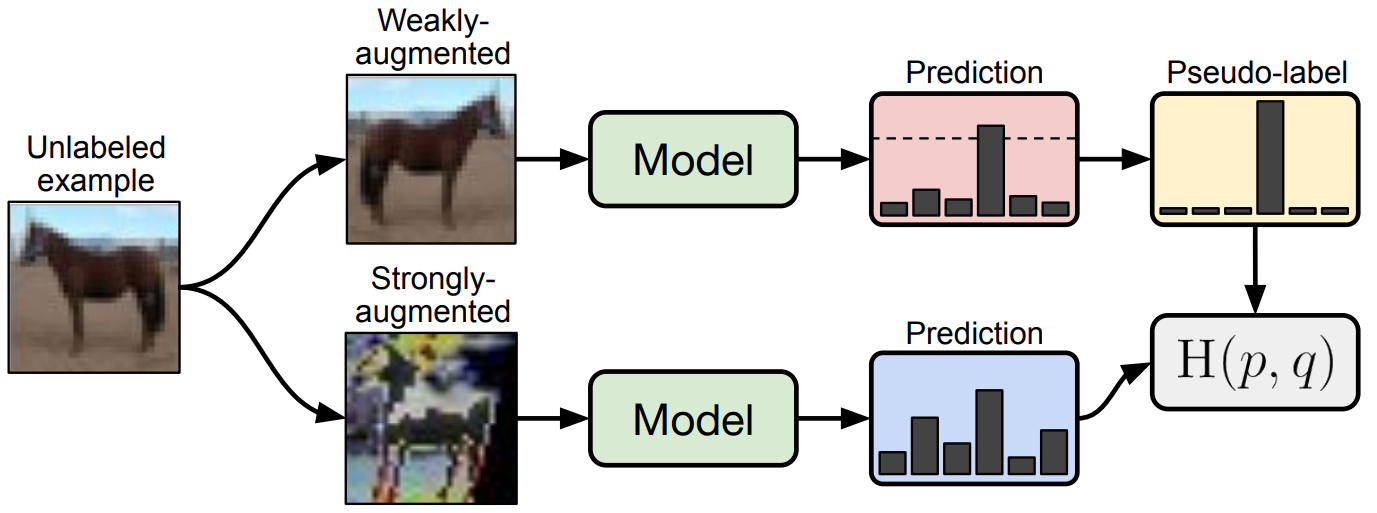
“FixMatch is a combination of two approaches to SSL: Consistency regularization and pseudo-labeling.”

FixMatch是一致性正则化和伪标签生成的结合。

Background

一致性正则化是当前最先进的SSL算法的重要组成部分(已在MixMatch中介绍)。

在这篇论文中，使用的超参数$\mu$就是MixMatch中的$K$。

伪标签生成是使用模型本身来获得无标签的虚拟标签数据。对某个无标签数据的输入，通过取 $\arg\max{output}$ ($output$是通过模型得到的输出，其维度即分类的类数)，作为该输入的伪标签。此时，对这个输出在$\max$的位置上有一定的阈值要求。相应的公式如下：

$$\frac{1}{\mu B}\Sigma^{\mu B}_{b=1}\mathbb{1}(\max(q_b)≥\tau)H(\hat{q}_b, q_b) \\ \hat{q}_b = \arg\max(q_b)$$

$H(p, q) $表示$p$与$q$之间的交叉熵。通过这种方式获得伪标签目的是为了降低熵值，鼓励模型对无标签数据做出“更加自信”(低熵)的推理。

其实MixMatch的Sharpen也在做类似的事情。

Our Algorithm: FixMatch

FixMatch有两个损失项：有监督损失项$l_s$和无监督损失项$l_u$。

$$l_s =\frac{1}{B}\Sigma^B_{b=1}H(p_b, p_m(y | \alpha(x_b))) \\ l_u = \frac{1}{\mu B}\Sigma^{\mu B}_{b=1}\mathbb{1}(\max(q_b)≥\tau)H(\hat{q}_b, p_m(y | A(u_b))) \\ \hat{q}_b = \arg\max(q_b) \\ q_b = p_m(y | \alpha(u_b))$$

论文中使用$A()$表示强增强，使用$\alpha()$表示弱增强。

$\hat{q}_b$表示伪标签，是由$u_b$弱增强后通过模型后得到的。然后对这个伪标签和强增强的$u_b$做交叉熵损失。$\tau$是限制获得伪标签的阈值超参数。与MixMatch相同，FixMatch同样得出如下损失值：

$$l_s + \lambda_ul_u$$

$\lambda_u$为无标签损失项的权重超参数。这个参数在多数SSL算法中会调的比较大，但在FixMatch中并不需要。在FixMatch训练过程中，开始时$\max(q_b)$经常性地会低于阈值$\tau$，随着模型的准确率上升，模型的预测会逐渐变得自信，此时会有更多无标签样例的$\max(q_b)$达到阈值$\tau$。在这样的趋势里，伪标签的会更自然地提供信息。

个人觉得FixMatch对伪标签价值的解读会比MixMatch更合理。

Augmentation in FixMatch

弱增强：50% 概率水平翻转(SVHN数据集除外)、至多 12.5% 比例的平移。

强增强：先基于AutoAugment的两种方法(RandAugment 和 CTAugment)，再使用Cutout。

Additional important factors

正则化尤为重要。论文中采用的简单权重衰减正则化(simple weight decay regularization)。

使用Adam优化器会导致低的性能，于是选择了标准带动量的SGD，其中动量部分选择标准动量或Nesterov动量没有太大差别。

关于学习率调整，采用余弦衰减，设置为$ηcos(\frac{7\pi k}{16K})$，$η$为初始学习率，$k$为当先训练步，$K$为总训练步。

采用指数滑动平均的模型参数进行最终性能测试。

如上是原论文Extensions of FixMatch部分以前的内容。

在原论文中，各个超参数的配置如下：

$\lambda_u$	$η$	$\beta$	$\tau$	$\mu$	B	$K$
1	0.03	0.9	0.95	7	64	$2^{20}$

收录一下其附录里的算法流程图：

两者对比

这里做一些理论上的总结。

相同点

• 都使用了数据增强方法来提高模型的泛化能力；
• 认为相同类别、相同增强来源的数据通过模型的输出应该相近，并基于这个观点进行训练；
• 都使用到了伪标签；
• 总的损失函数写作有监督和无监督损失项的加权和；
• 对于有监督项，都采取交叉熵损失函数。

不同点

• MixMatch对所有训练数据只采取了弱增强，FixMatch对有标签数据采取弱增强，对无标签数据同时进行了弱增强和强增强；
• MixMatch通过MixUp步将两个部分的数据混合在一起，FixMatch分开处理；
• MixMatch想要拉近相同类别下的数据(有标签和无标签都包含在其中)，FixMatch则想要拉近弱增强下和强增强下的同一个无标签数据。
• MixMatch一开始就把无标签数据纳入训练，FixMatch则对无标签弱增强数据的预测概率设置了阈值，在模型变得自信后，逐渐采纳那些大概率预测准确的无标签数据；
• MixMatch将无监督项的权重设得很大以平衡两个部分(与多数SSL算法相同)，FixMatch则不需要分配很大的权重；
• 对于无监督项，MixMatch采取了更敏感的L2损失，FixMatch则使用了与有监督项相同的交叉熵损失。